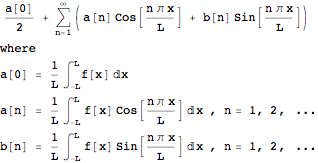
Fourier Series Notes

f[x] defined on [-L, L] has Fourier series

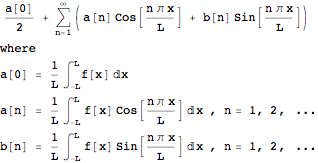
There are many sufficient conditions for Fourier series to converge.  Here are some: f and f' are piecewise continuous;   f is pieceise smooth; f is piecewise continuous with finite one-sided  limits at the endpoints of each subinterval; f is pieceise continuous with each piece monotone.

If f is continous at c, the Fourier series for x=c converges to f(c).
If f is not continous at c, the Fourier series for x=c converges to.

f[x] defined on [0, L] has Fourier cosine series

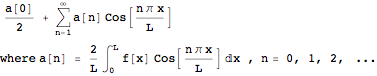
f[x] defined on [0, L] has Fourier sine series

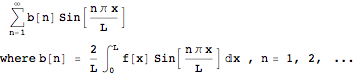
Created by Wolfram Mathematica 6.0  (24 January 2008)